Analysis of a web cam image downloaded by Gavin Joth

Frame 2 of the series of 6 images. Original condition.
Analysis of a web cam image downloaded by Gavin Joth

Frame 2 of the series of 6 images. Original condition.
Introduction
Loch Ness is the subject of international interest, and just about every "monster sighting" eventually makes it's way into the media. Many researchers who do not live locally - naturally the vast majority - have depended on these media reports for their information. Local researchers have the unique facility to visit the locus of the incident, make further observations and measurements, and even attempt reconstructions of the original event to produce more reliable data. Without this follow-up work the source material for future subject literature would simply remain a collection of witness statements, original photographs, and press speculation spiced with "expert" comment from people who are sometimes very highly qualified in some fields but woefully uninformed in this one. My associates and I regard it as our obligation, as investigators, to examine these events as minutely as we can for future reference, and make our findings freely available to our more distant colleagues.Background
In late December 2000, as a result of a correspondence starting in October, Mr Gavin Joth kindly sent me copies of 6 pictures he had downloaded on Tuesday 20th June 2000 from the Scotland-Online web cam situated at Temple House, near to Drumnadrochit. At the time he said he was "pretty convinced we are looking at a big grey seal in the pictures" (pers comm, 28th December 2000) and I had expressed an opinion that it was more likely to have been a boat, for a variety of reasons.Early in 2001 it was announced that the pictures had been chosen as joint winners of the annual William Hill Nessie Picture of the Year Contest (along with Melissa Bavister's picture, analysed elsewhere on this web site) and had each been awarded a £500 William Hill prize by the competition judges Mr Gary Campbell, President of the Official Loch Ness Monster Fan Club and Mr Mikko Takala, owner of the Nessie on the Net web site (which hosts the Fan Club).
Anlaysis methods
Image analysis can take several forms, being either practical - involving a reconstruction of the event and photographing objects of known size in the same location as the "unknown" object, or a purely mathematical treatment working from maps, photographs, gps and other data (including local knowledge). Ideally, both methods should be carried out.I will describe here the latter method, as the practical reconstruction of the event and the deductions made from it have already been carried out by the Loch Ness Project, and part of the procedure has already been transmitted as part of a television documentary early in 2002.
An introduction to the mathematical method is already available on this web site, and I will simply outline the differences necessary in this particular analysis, and progress as it is made.
The Procedure
Of the 6 pictures sent to me by Mr Joth, I will deal only with the one he regards as being the best, shown above. It was only 383 x 287 pixels when received, and so I enlarged it by "resizing" it using Adobe Photoshop, and altering the contrast and sharpness. The only reason for this was to give me a better chance of measuring boundaries and dimensions more accurately.Establish the field of view

a reproduction of the working drawing
The web cam from which the pictures were downloaded is programmed to pan tilt and zoom to give a variety of different views, so the only fixed criteria are its location - established by a portable Global Positioning System device (the building to which it is attached is also shown on Ordnance Survey maps), and whatever is visible in the picture.As it was taken with a zoom lens, we must first establish the angle of view. This would sometimes be done using the known size of Urquhart Castle tower, but as this is not recognisable under these lighting conditions another method was used. Examining an Ordnance Survey Map of the area, a line was drawn from the camera location, touching the end of the promontory where Urquhart Castle stands (which I shall call Castle Point), and on across the loch and into the hills beyond. This showed that the height of the hills visible in that direction was 250 metres, and the peak was at a distance of 4500 metres. This is shown on the picture above as a yellow line.
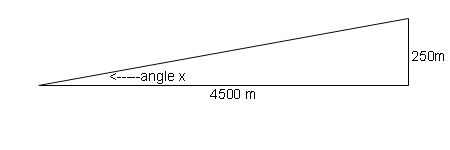
calculating the field of view - measure a known objecttangent of angle x ( tan x ) = opposite side / adjacent side = 250 / 4500 = 0.0556
angle x is therefore inverse tangent .0556 = 3.1798 degrees (use the scientific calculator in "accessories")
In my working picture the length of the yellow line was 155 pixels out of a total picture height of 1614 pixels, so this gives us the vertical angle of view of the camera system as 1614 / 155 x 3.1798 = 33.111degrees.
This is important, because we can now measure by how many degrees the unknown object is lower down the image than the shore at the Castle Point.Locate the unknown object within the scene
We know that 1614 pixels = 33.111 degrees, so we can draw a line level with the object and another line level with the castle point and measure the distance between them. This turns out to be 248 pixels. Or 248 / 1614 x 33.111 degrees, which is 5.09 degrees. We know from the map that the castle tower is 1440 metres from the camera, so we are nearly home.
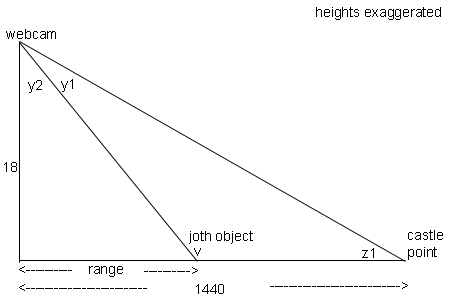
calculating the rangeWe have to work out all the angles and lengths of sides and we can do it!
Angle z1 comes from tan z1 = 18 / 1440, = 0.0125, so inverse tan = 0.71616 degrees.
All the angles in the corners of the big triangle add up to 180, and one of them is 90, so...
Angle y1 plus angle y2 must equal 90 - 0.71616 = 89.28284 degrees.
But we know that the Joth object is 5.09 degrees lower down the picture than the castle point...
So y2 must be 89.28284 minus 5.09 = 84.19384 degrees.
We now know two things about the little triangle so we have it nailed....
tan y2 = range / 18, so 18 times tan y2, or 18 x tan 84.19384, = 177 metres range.
It's not very far away is it? So how big might it be?Calculate the size of the object
We know the range of the object is 177 metres, but the image is still 33.111 degrees high and made up of 1614 pixels. Imagine a huge sheet of glass standing vertically in the loch 177 metres from the camera. How high will it be?
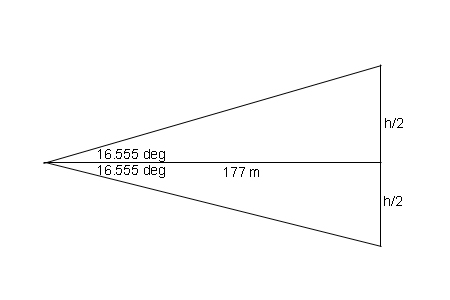
calculating the size of the fieldThe triangle is divided into two right angle triangles. h/2 - half of the height of the field of view at 177 m
is given by 177x tan16.555 (being half of 33.111) = 52.61, so the full vertical field is 105.22 m.But this is made up of 1614 pixels, so each pixel is 105.22 / 1614 = 0.0652 m , and they are square.

counting the pixelsTo measure the object - count its pixels. Just zoom in and do it. I make it about 18 high and 49 long and , so what is visible in the picture seems to be 18 x 0.0652 m =1.17m high, and 49 x 0.0652 m = 3.19m long.
Without knowing what shape it is and which direction it is pointing, that is all that can be said. We are lucky therefore that it is leaving a wake behind it consisting of three elements - two "vee" arms and a central line of disturbed water.Speculate on its identity
So where does this take us? Mr Joth favoured a large grey seal, citing the grounds that one was seen nearby in the same month as he saw his object. I favoured a small grey inflatable boat -specifically an Avon Redcrest, on the grounds that practically every holiday cruiser that stays overnight in Urquhart Bay Harbour (located 200 metres away) is equipped with one for safety purposes and also for exploring the shoreline. They are equipped with removable outboard engines, so sometimes they are rowed, and sometimes they are motorised. There are frequently more than a dozen of these little dinghies in the area each morning and evening, and a trip across the bay is very appealing. The time, 8.30 p.m., and day of the week, Tuesday, fit nicely with known visitor activity. Looking at the picture above, you may decide for yourself if the object looks like a seal or an inflatable boat or even something else.Whatever it is, it is making steady progress, continually above the surface, at an angle of about 30 degrees across the picture. Seals, in my experience, generally spend very little time on the surface unless eating something, and then they are usually stationary.
So how big is an Avon Redcrest? It is 2.74 metres long and 1.48 m wide. Check for yourself. Viewed obliquely at an angle of 30 degrees off the stern you would see both part of the length and part of the stern...specifically, (2.74 x cos30 degrees) = 2.37m of its length plus (1.48 x cos 60 degrees) = 0.74 of its beam making a total of 3.11 m
Conclusion
Proof of the identity of this object is not available. Given the close resemblence in size, location, and behaviour to a holiday cruiser's dinghy with a small outboard engine, and the knowledge that such boats would be in the area, the overwhelming probability is that the pictures do show an inflatable dinghy with an outboard engine.
I would be delighted if the data supported Mr Joth's seal explanation, but on present calculations I suggest that this does not seem to be the case. I am grateful to Gavin Joth for his generous sharing of information which has made my analysis possible, and his reponse to a pre-publication version of this web page has included an equally generous acknowldgement of its plausibility. Thank you, Gavin.Dick Raynor. March 2002
Back to Index
Bavister Picture Analysis
Gray Picture Analysis (next winner of the William Hill Prize?)
Avon Redcrests atop Caley Cruisers in Urquhart Bay harbour.
Diagrams & Text Copyright © Dick Raynor 2002. All Rights Reserved
Version1.2 March 8th 2002
Criticism
I have recently been criticised by the "President" of the "Official Loch Ness Monster Fan Club" for going to great lengths to "disprove this picture". I regard this as a mischievous criticism - my only interest is in identifying the objects in alleged Nessie photographs wherever possible, to enable genuine researchers to separate the wheat from the chaff, and focus their investigations accordingly. Such criticism is especially inappropriate in this case where the speculation is only between two perfectly mundane explanations, seal and boat.