and the "Roy Johnston Photographs"
On Sunday 27th May 2001 the "Mail on Sunday" newspaper carried some photographs taken on Loch Ness by Mr. James Gray of Invermoriston, who was described as a "semi-retired professional photographer".
These pictures had been in the hands of potential buyers for about two weeks prior to their eventual publication, having been taken on May 9th, and I had been given the opportunity to study full frame colour enlargements of all five of them. The contact strip also seen showed two spoiled frames at the start of the film where the film was loaded, followed by five frames taken in the middle part of the loch showing a curved and elongated object in the act of changing from an elevation angle of around 55 degrees to horizontal in a motor-driven sequence which we are told took about 2.5 seconds. Unexposed frames follow on after the exposed ones, indicating that there was unused film remaining in the camera and the opportunity to take more pictures. The camera used was stated to be a Nikon 801 with a 35-70mm zoom lens in the 35mm setting.*(see below)
Of the five relevant frames three show the object rotating anti-clockwise towards the loch surface, the fourth shows it on the surface and the fifth shows it also on the surface but slightly higher in the water.
The curvature of the object is consistent in all the frames, suggesting no bending during the sequence. There is a curious region of increased diameter about one third of the length from the interface with the loch surface, and the "end" of the object seems to be of reduced size or diameter compared to the rest of it.
At first glance, it appears rather difficult to "measure" such photographs, but I will bravely "have a go"!
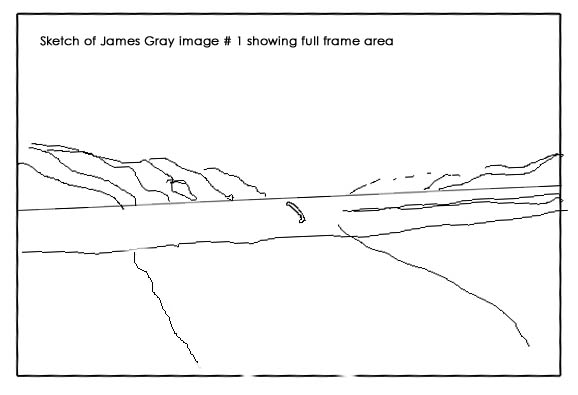
Here is an outline sketch of the (believed) full frame of the first image. It shows that the camera was not quite level when the pictures were taken. Ideally I would prefer to use a print or scan of the entire frame including the film perforations, but requests to the photographer have not yet received any acknowledgment.
An introduction to measuring web cam pictures is here.
We need to work out a number of parameters to measure
the pictures.
1, the angle of view of the camera
2, the height above water surface of the camera
3, the distance to the horizon
4, the angle that the object is below the horizon
5, the distance to the object
6, the size of the object and
7, any implications deriving from 5 and 6.
Item 1 - the angle of view of the camera.
We first need to work out the angle of view of the camera - lens combination. We are told the camera is a Nikon 801 35mm full-frame camera, and that the lens was set at 35mm focal length.
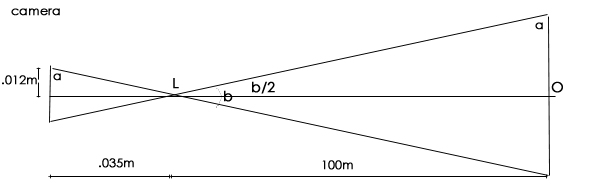
A 35mm negative frame is 36 mm wide and 24 mm high when used in the normal orientation. Above is a diagram showing the negative in the camera, the front of the lens at L, and the object O at a nominal distance of 100 metres. When set to "infinity", the optical centre of the lens is one focal length ( in this case 35mm or 0.035m) from the film. The other side of the diagram is a notional image plane 100 metres away. The first thing to notice is that we have two sets of similar triangles - the angles are the same, only the lengths of the sides differ.
We wish to calculate the vertical field of view in degrees.
in the camera, tan a = "opposite over adjacent", or 0.035 / 0.012. or 2.916667
so angle a = 2.916667 INV tan = 71.075 degrees.
So b/2 in the "image" triangle = 90 minus 71.075 = 18.92 degrees,
So the vertical angle of view in any photo taken at this setting is 2x18.92 = 37.85 degrees.
Item 2: The Height of the camera above the water.
Examination of the boat (assumed to have been used) in the published photograph suggests that the photographers feet were probably at or very near water level when the photographs were taken. If the photographer was sitting down, then the camera would have been about 1.2 metres above water level. If he had stood up to take the pictures ( as is understood to be the case) the the camera height would have been about 1.5 metres. Both of these measurements will be used with the sitting data given first with the standing data given afterwards in brackets (parentheses).
Item 3: The distance to the horizon.
Using a Nautical Almanac, one can look up tables which reveal that the horizon apparent to an observer whose eye is 1.2 metres above water level is at a distance of 4260m, while for a height of 1.5 metres it is at 4760m.
Item 4: The angle that the object
is below the horizon.
We can now go to the outline tracing of the photograph
and measure the angle below the horizon for the base of the floating object.
The picture used for measurement is tilted at an angle
of about 2.4 degrees to the horizontal, but we can tilt our measuring to
allow for this.
The height of the entire frame is 360 pixels in the example
I used for measurement, and we have already established that this is equivalent
to a vertical angle of view of 37.85 degrees. So each vertical pixel
(or horizontal one for that matter) represents an angle of 37.85
/ 360 degrees. My measurements suggest that the water-line of the
object is 25 pixels below the horizon, so this equates with 25 x 37.85
/ 360 degrees or 2.63 degrees below the horizon.
Item 5: The distance to the object
We can now construct a diagram with a couple of triangles to solve - without too much difficulty.
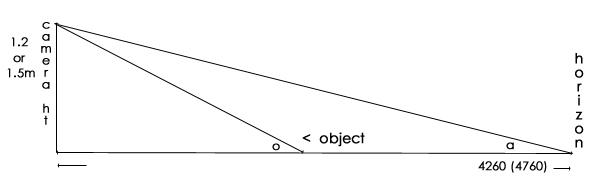
the angle "a" at the horizon is the first to be calculated,
and it is given by tan a = 1.2 (or 1.5) / 4260 (or 4760)
and these work out to give tan a as 0.00028169 or 0.00031313,
making angle a = INV tan these values, or 0.016139
or 0.018055 degrees.
Angle at "o" then becomes 2.3+ these values, which are
2.316139 or 2.318055 degrees.
The distance from the camera to
the object "o" then is worked out as follows:
tan o = 1.2 (or 1.5) divided by range, so range = 1.2
(or 1.5) / tan "o"
= 29.6689 m or 37.0555m - say metres
(100 feet) or metres (121 feet)
Item 6: The size of the object
Now that we know the range, (or at least two choices of range) we can easily calculate what a pixel is "worth" at that distance, and measure the various dimensions of the object.
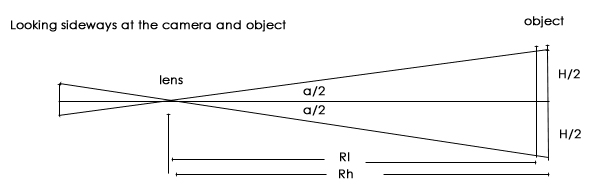
Further up the page we worked out that the vertical angle of view of the camera - lens combination (as stated by Mr. Gray), a/2 in this diagram. = 18.92 degrees, so we can now go on to work out H/2 for each of the two ranges we are interested in - Rl is the range with camera lower (1.2m) and Rh is the range with the camera at the higher distance, 1.5 metres above water level.
Using the familiar tangent formula tan (a/2) = (h/2)
/ Rl or Rh, we re-arrange the equation in the normal way to get h/2 = tan
(a/2) x Rl (or Rh)
= tan 18.92 x 29.7 or
tan 18.92 x 37.0
= 0.34277 x 29.7 = 10.180m or 0.34277 x 37.0 = 12.682m
So the total height of the image at the ranges in question is twice the above values, that is
20.36m or 25.36m, depending on whether the photographer was sitting or standing. The length of a single pixel in the 360 - pixel image I am using is therefore 20.36 / 360 = 0.057m, (low) or 25.36 / 360 = 0.070m (high).
The object in the first frame appears to be about 27 pixels long,
i.e. 27 x 0.057m = 1.539m (low) or 27 x 0.070 = 1.902m (high) - say 1.5m (59 inches) or 1.9m (75 inches) long
and appears to have visible thickness averaging 3.5 pixels = 0.1995 or 0.245m. ( 7.9 inches or 9.6 inches)
Item 7: Implications of these size estimates.
If Mr. Gray was standing up in his
boat -as is believed to be the case - , then the part of the
object out of the water is about 1.9 metres long
and nearly
25 cm wide. If cylindrical, and
of neutral buoyancy, its mass would be about the same as a similar sized
cylinder of water, i.e. 3.142 x 0.12 x 0.12 x 1.9 = 0.0859 cubic metres
or 86 kg.
If the smaller size estimate is closer to the mark, then
the volume would be
Pi x radius squared x height (all in metres) = ( 3.142
x 0.2x0.2x1.54) =
0.048 cubic metres = 48 kg
Further calculations suggest that the water at the bottom of the frame is only 4.48m from the camera, indicating that the pictures were taken over the side or stern of the boat. If the photographer was in the stern as stated, and took the photographs in the direction of the bow of the boat, both the bow and the oarsman would be visible in the photos.
Mr. Gray's own estimate of the objects size at "about 6 feet (1.83m )out of the water" is remarkably consistent with my own "standing" value (1.9m) but his reported distance from it "about 150 yards" ( 137m) is 100 metres greater than my "measured range".
V1.1- 6th June 2001
Mr. Gray has kindly corrected a few points in the narrative which I mis-reported in the first version of this page. Specifically, the quoted lens focal length setting of 35mm may not be correct, and may have been at the 70 mm setting, or anywhere in between, and secondly, he reports that the shape of the object did change prior to his taking the series of photographs.
The implications of the different focal length setting are quite interesting:
Calculations are for 70 mm, and obviously intermediate setting would give values between those for 35 and 70 mm.
Vertical angle of view in the full frame picture is 2x INV tan (0.012 / 0.070) = 19.45 degrees
Waterline angle below horizon 25 pixels / 360 pixels x 19.45 = 1.3511 degrees
Camera elevation confirmed as "standing up" (1.5m)

Angle at horizon = INV tan 1.5 / 4760 = 0.000315126 degrees
Angle to object waterline below horizon = 1.31511, so
Angle at "o" = 1.315425126 degrees (again, we'll deal with the accuracy issue at the end!)
tan "o" = 1.5 / range, so range = 1.4 / tan o, = 1.5 / 0.02296 = 65.32 - say about 65 metres.
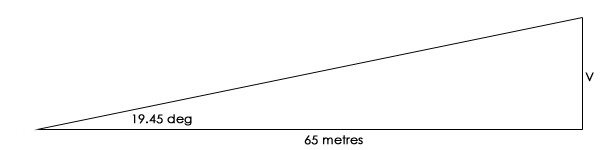
The vertical field of view of 19.45 degrees at a range of 65 metres is given by:
tan 19.45 = V / 65, so 65 x tan 19.45 = V = 22.95 metres
and the length of the object is 27 pixels in a 360 pixel high frame, so is 27 / 360 times this value, or 1.72 m (68 inches)
This rather bizarre result, only 18 cm or 7 inches different from the calculations based on a focal length of 35mm suggests that perhaps the focal length doesn't matter!
To test this, let us pretend that the pictures were taken with a 200 mm lens.
The vertical angle of view becomes 2x INV tan .012 / .200 = 6.867 degrees
Angle at the horizon is still = 0.000315126 degrees
Waterline angle below horizon 25 pixels / 360 pixels x 6.867 = 0.476893 degrees
Angle at object becomes 0.000315126 degrees + 0.476893 degrees = 0.480044 degrees
Range is given by 1.5 / tan 0.480044 = 179.03 metres
Vertical field at 179 m is given by V = Range x tan 6.867 degrees = 21.56 metres
So length of object is 27 / 360 x 21.56 = 1.62 metres ( 64 inches)
So, for some reason which I cannot
at present explain (come on readers - help me out here!) the focal length
doesn't matter much , giving values for object length varying only between
1.9 metres with a 35mm lens, 1.72m with a 70 mm lens, and 1.62m with a
200 mm lens. It may be that it doesn't matter at all, and the slight variations
are due to some other over-simplifications I have made. Time may tell.
This set of photographs came to my attention when I was asked to examine them for a leading British newspaper on Friday 30th August 2002. They were purported to have been taken on 21st August 2002 by Mr. Roy Johnston, from Loughton, Essex, England. He was "taking a breather on his long drive home" from the Clansman Hotel to Essex and had stopped in a lay-by near Inchnacardoch to enjoy the view. After standing there for a few minutes, suddenly the creature appeared. "I just started taking pictures. I don't know anything about photography. It's just an automatic Nikon that I've had for years." The camera had fortuitously been "hanging round his neck" at the time. After several more minutes Mr. Johnston scrambled back up to the lay-by to tell his wife, but she refused to believe him. "It wasn't until we finally got the pictures developed when we got back home that she finally believed me."
The Photographs
There are eight of them in the Nessie sequence, but they
are preceded by a few pictures of Urquhart Castle. Part of Frame 1 is
here.
Black and white versions of four of the pictures are
here.
If you click on a small picture you will be taken to a larger version.
Size and distance.
Using standard methods involving known objects on the
opposite shore, I have calculated the range to the object as being about
42 metres, and the height to the top of the head as being about 72 cm (28
inches).
The Nessie Sequence:
The first, third, fifth and sixth pictures were published
by the Scottish Daily Mail on Saturday September 7th 2002.
Frame 1 shows an arched "neck", with a slightly bulging
"head" on the end of it, extending in a quarter circle to the right and
entering the water vertically. The "neck" appears to be of constant diameter,
just about 12 cm, or a little less less than five inches.
Frame 2 shows what appears to be the same object in the
form of a hoop, with the tip of the "head" in the water.
Frame 3 shows the same object with a different wave background
Frame 4 shows the neck now almost flat on the water
Frame 5 shows the neck slightly further out of the water
Frame 6 shows a large splash
Frame 7 shows another splash
Frame 8 shows very little except waves.
Comments.
Where to begin? The Nessie Sequence is stated to have
been taken on August 21st. Unfortunately it was flat calm on that day -
the snaps show a Force 2 or 3 wave scene.
The pictures of Urquhart Castle at the beginning of the roll of film were taken prior to substantial landscape improvements which were completed in early July. I know traffic can be rather slow on the A82, but it shouldn't have taken over 50 days to travel the 20 or so miles between the Clansman Hotel and the place between Inchnacardoch and Invermoriston, where the pictures were taken, at Grid Reference NH 40377 12200.
Roy Johnston is quoted as stopping in the lay-by to admire the view. There is no view of the loch from this lay-by - it is obscured by trees, as is the view from neighbouring lay-bys.
The pictures should have had blooming heather in the background if they had been taken in mid to late August. They do not.
The pictures are remarkably steady for someone taking snaps of a monster only 45 yards away - and the shoreline is in the same position in each picture. I suspect these were taken using a tripod.
The pictures show no real interaction between the object and the water - except for the obvious splashes in frames 6 and 7 where the "Nessie" is not visible. I see no real evidence that the object was there when the pictures were taken - no waves, no wakes. It could be a computer generated sequence.
However, I do see a strong similarity between these pictures and those taken by James Gray, discussed above, both in the type of object photographed and the handful of professional quality snaps submitted.
James Gray moved back to London after his financially successful foray into monster photography, and now, according to the "News of the World", runs a professional photo lab in London. By a strange coincidence, this lab is the one chosen by Roy Johnston to develop his snaps, and James Gray is even acting as his agent!
Conclusions
If, as seems inescapably true, the pictures were not
taken in August 2002, then there is equally no reason to believe that they
were taken by Mr. Johnston at all. Given the confusion about lay-bys, weather
conditions, castle improvements, etc., one would be justified in dismissing
them as a load of baloney, except for one thing. If they were not taken
by Mr. Johnston on this visit to the area, who did take them? James Gray
perhaps? And if these are fakes, and are similar to the pictures he took
last year, are we seeing the emergence of a twenty-first century Frank
Searle?
References:
Scottish Daily Mail, Saturday September 7th 2002
News of the World, Sunday, September 8th 2002
Postscript
On 16th September GUST published a flimsy and scurrilous
attempt at counter argument at http://www.cryptozoology.st/
My measured response to the points raised is to be found
here.
There was then another page of argument published here...
which I have commented on here.
Post Postscript
Those sufficiently interested will have noticed the Global
Underwater Search Team's heavy reliance on (and misinterpretation of) the
records from the Meteorological Office. The images of Urquhart Castle
(which Mr. Gray, agent for Mr. Johnston, would not allow to be published)
preceding the "Nessie" pictures were taken before landscaping work altered
the appearance of the edges of the footpaths on the castle site. Furthermore,
Mr. Johnston's story as reported in the "News of the World", Sunday, September
8th 2002, told how he had "snapped the castle the previous day"- which
would have been August 20th. The paper also reports that hotel records
showed that Mr. Johnston stayed in two hotels on Loch Ness-side on the
Sunday evening and Monday evening, August 18th and 19th, but not on the
20th.
The pictures of the castle show a sunny afternoon scene
on a windy day with many breaking waves clearly visible. The time is between
1530 and 1600.
The weather records for this time on the relevant days
is as follows:
Sunday August 18th Cloud 8 oktas,
continuous moderate rain , wind 0 knots
Monday August 19th Cloud 7 oktas,
cloudy, wind 4 knots
Tuesday August 20th Cloud 5 - 6 oktas,
rather cloudy, wind 3 - 4 knots
As if the scenery being "wrong" was not enough to damn
the story, the weather reports do not support it either.
Back
to Index
Bavister
Picture Analysis
Joth Picture
Analysis